
|
SICUREZZA NELL'INDUSTRIA DI PROCESSO
Fondamenti |

|
SICUREZZA NELL'INDUSTRIA DI PROCESSO
Fondamenti |
| HOME |
| ELEMENTI INTRODUTTIVI |
| CASI STORICI |
| SCHEDE DI SICUREZZA |
| ANALISI DI RISCHIO |
| GLOSSARIO |
| LEGGI E REGOLAMENTI |
| PUBBLICAZIONI |
| LINK |
| Radiazione termica da fiamme libere |
|
Le fiamme creano danni locali, che possono essere contenuti tramite un efficiente e tempestivo sistema antincendio, ma possono essere causa anche di danni a distanza dovuti all’azione del calore irradiato. Questo aspetto del fenomeno è particolarmente importante nell’industria di processo perché la presenza di sostanze tossiche e/o infiammabili raramente si trova all’interno di una sola parte d’impianto o in una zona circoscritta dello stabilimento e dunque prevedere gli effetti da radiazione termica a distanza equivale a prevenire un probabile effetto domino. Si pensi, ad esempio, ad un parco serbatoi di prodotti petroliferi. L’incendio di un serbatoio o un incendio accidentale nelle vicinanze dell’area potrebbe surriscaldare un altro serbatoio, per sola radiazione termica senza necessità di attendere la propagazione delle fiamme, e questo a sua volta incendiarsi o esplodere e così via, con un effetto domino disastroso. Qui di seguito si esaminano i principali aspetti del fenomeno con un accenno ai modelli di calcolo semplificati ma sufficienti per una valutazione di massima. Il calore che raggiunge un target per radiazione termica (q in W/m2) si può calcolare con la relazione : 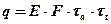 ove E è la potenza emissiva della superficie della fiamma (in W/m2), F il fattore di vista geometrico della fiamma rispetto al target, &àx03bd;a è la trasmissività in atmosfera e νt è l’assorbività del target. La potenza emissiva si calcola con la legge di Stefan-Boltzmann quando è nota la temperatura di fiamma (T in °K): 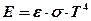 ove: ε = emissività (valore assunto generalmente unitario) σ = costante di Stefan-Boltzmann (5,67x10-8 W/m2°K4) Per temperature di fiamma comprese tra 1.150 e 1.450 °K la potenza emissiva massima può variare tra 99 e 250 kW/m2. Ad esempio, per la benzina E=110 ÷130 kW/m2. Il fattore di vista porta in conto la distanza della fiamma dal target e l’orientamento reciproco per cui va definito caso per caso. La trasmissività dipende da sostanze presenti lungo il tragitto dalla fiamma al target capaci di assorbire parzialmente la radiazione termica. In pratica si tratta del vapore acqueo (αν) e del biossido di carbonio (αc) in quanto è difficile imbattersi in situazioni ove vi sia una presenza in concentrazioni significative di altre sostanze con simile capacità di assorbimento della radiazione termica. In sostanza: 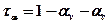 Senza entrare nei dettagli del calcolo di questi parametri, per il quale si rimanda alle pubblicazioni del TNO, è sufficiente sapere che αν dipende dalla pressione parziale del vapore e questa a sua volta dalla temperatura e dall’umidità relativa, ma anche dalla temperatura della superficie radiante e dalla distanza del target. Orientativamente αν può assumere valori variabili tra zero e 0,4. Analoghe considerazioni valgono per che incide meno sull’intercettazione della radiazione termica assumendo valori che possono variare tra zero e 0,05. Infine, l’assorbività dal target in linea di principio varia tra 0 e 1. Per un uomo nudo è 1, mentre per un vigile del fuoco equipaggiato con tuta ignifuga esso è trascurabile. In pratica, in uno stabilimento industriale gli addetti sono vestiti e in alcuni casi hanno in dotazione equipaggiamenti idonei per far fronte ad eventi accidentali oppure hanno la possibilità di ripararsi all’interno di rifugi da poter raggiungere in pochi secondi. Per quanto riguarda le apparecchiature, per prevenire surriscaldamenti si adottano sistemi di bagnatura continua e/o vernici e colori capaci di riflettere la radiazione incidente. Spesso è difficile conoscere o calcolare la temperatura di fiamma come nel caso di miscele di idrocarburi, oltre alla circostanza che ai fini della radiazione termica trasmessa a distanza è difficile calcolare anche il peso della CO2, del vapore e degli eventuali incombusti. In tal caso è facile conoscere invece il calore di combustione il quale si calcola come prodotto della portata massica ( 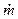 in Kg/s) per il calore di combustione (hsub>c in J/Kg). in Kg/s) per il calore di combustione (hsub>c in J/Kg).Di questo calore solo una frazione (η) si disperde per irraggiamento per cui : 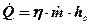 Questo avviene attraverso tutta la superficie di fiamma (Af) che non sempre è facile da quantificare. Il calcolo si semplifica nel caso ipotetico di una fiamma libera “puntiforme” e dunque di una superficie sferica: 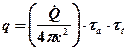 ove: 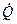 = frazione (η) del calore di combustione trasmesso per irraggiamento = frazione (η) del calore di combustione trasmesso per irraggiamento να= trasmissività in atmosfera νν = assorbività del target x = distanza tra la fiamma e il target Fireball Una palla di fuoco si genera quando si ha una rottura istantanea di grosse dimensioni di un serbatoio di gas liquefatto che nella fase di espansione prende fuoco immediatamente prima di miscelarsi con l’aria per cui la fiamma avvolge tutta la massa di combustibile sollevandola da terra per effetto della densità. In letteratura si trovano diverse formule empiriche più o meno equivalenti, per quantificare le dimensioni di queste palle di fuoco e la durata della combustione, ricavate con prove sperimentali in campo. Il centro di ricerche TNO olandese suggerisce : r = 3,24 m0,325 t = 3,24 m0,26 ove r ( in m) è il raggio della palla di fuoco, t (in sec) il tempo necessario perché la fiamma si estingua e m è la massa (in Kg) di combustibile. Ad esempio, si assuma che un’autocisterna di 45 m3 di volume, riempita all’85% di LPG (essenzialmente propano), subisca un incidente con una conseguente rottura catastrofica alla quale segue un BLEVE che evolve in una fireball. Il rilascio è di 38,25 m3 pari a 19.200 Kg ( &àx03c1; =502 kg/m3) e l’evento da luogo ad una fireball del quale si può calcolare il raggio iniziale e il tempo si esaurimento: 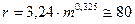 (metri) (metri) 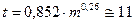 (secondi) (secondi)La potenza emissiva per il propano si può assumere in 196 kW/m2. Quanto al fattore di vista questo dipende dalla distanza e dalla posizione più o meno decentrata del target il quale viene a trovarsi esposto solo ad una parte della superficie della sfera e dunque della potenza emessa. Per questo in letteratura sono riportati grafici che aiutano a sviluppare queste valutazioni e consentire di tracciare una mappa a livello del suolo di curve iso-radiazione incidente. Poolfire Nel caso di una fiamma che si sviluppa da una pozza per ricavarne la superficie si può assumere che la conformazione sia pressoché cilindrica. Una relazione sperimentale, ricavata dal TNO, tra altezza di fiamma (hsub>f) e diametro della stessa (df) è : 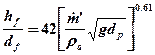 essendo dp il diametro della pozza (che in genere è uguale a quello della fiamma), g l’accelerazione di gravità, ρa la densità dell’aria (Kg/m3) e 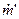 la portata massica del combustibile per unità di superficie del pool (Kg/m2s). la portata massica del combustibile per unità di superficie del pool (Kg/m2s).In pratica il rapporto tra altezza e diametro della fiamma diminuisce all’aumentare del diametro perché diventa sempre più difficile l’apporto di ossigeno al centro del pool. Per avere un ordine di grandezza si consideri che per diametro del pool di 10 m il rapporto è circa unitario, mentre per diametro di 1 Km (ad esempio una chiazza nel caso da versamento in mare di idrocarburi) il rapporto scende a 0,4. Per il calcolo della portata massica di combustibile, che corrisponde alla quantità di liquido che evapora, per liquidi con punto di ebollizione maggiore della temperatura ambiente, il TNO suggerisce di adottare un semplice rapporto tra calore di combustione e calore di evaporazione al quale va aggiunto il calore necessario per riscaldare il liquido sino alla temperatura di ebollizione : 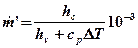 ove: hν = calore latente di evaporazione (in J/Kg) cp calore specifico del liquido (J/Kg °K) ΔT = differenza tra temperatura del liquido e temperatura di ebollizione Per liquidi con punto di ebollizione minora della temperatura ambiente il termine cp ΔT scompare. Ove si voglia avere un valutazione della durata di combustione di un poolfire si può assumere che la portata massica specifica sia pari alla velocità di abbassamento del livello della pozza ( 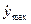 ) per la densità del liquido : ) per la densità del liquido :
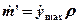 Poiché la pozza cambia nel tempo si può assumere una variazione esponenziale della velocità di abbassamento del livello: 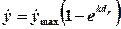 ove k è un coefficiente di estinzione dell’ordine, ad esempio, di 2,7 per il butano. Valori di 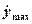 per idrocarburi variano tra 0,5 e 1 cm/min (0,7 per LNG, 0,8 per butano, 0,2 per metanolo, 1,4 per idrogeno). per idrocarburi variano tra 0,5 e 1 cm/min (0,7 per LNG, 0,8 per butano, 0,2 per metanolo, 1,4 per idrogeno).Quella appena esposta è una traccia di modello che può essere reso più complesso introducendo ad esempio il caso in cui il pool venga alimentato da nuovo combustibile e/o che vi sia uno scambio significativo di calore anche attraverso il terreno e/o che vi sia presenza di vento, ecc. Jetfire Il jetfire è la fiamma della cucina di casa, ma anche della fiaccola degli impianti petroliferi e petrolchimici. |